1. Menemukan Konsep Nilai Mutlak
Ilustrasi:
Kegiatan pramuka adalah salah satu kegiatan
ekstrakurikuler yang diadakan di sebuah sekolah.
Sebuah grup pramuka sedang belajar baris berbaris
di lapangan sekolah pada hari Sabtu. Sebuah perintah
dari pimpinan pasukan: “Maju 4 langkah, jalan!”, hal
ini berarti jarak pergerakan barisan adalah 4 langkah
ke depan. Jika perintah pimpinan pasukan: “Mundur
3 langkah, jalan!”, hal ini berarti bahwa pasukan akan
bergerak melawan arah sejauh 3 langkah. Demikian
seterusnya.
Besar pergerakan langkah pasukan tersebut merupakan
nilai mutlak, tidak ditentukan arah. “Maju 4 langkah”,
berarti mutlak 4 langkah dari posisi diam dan “mundur
3 langkah, berarti mutlak 3 langkah dari posisi
diam. Dalam hal ini, yang dilihat adalah nilainya,
bukan arahnya. Lebih jelasnya, mari bersama-sama
mempelajari kasus-kasus di bawah ini.
CONTOH:
Seorang anak bermain lompat-lompatan di lapangan. Dari posisi diam, si anak
melompat ke depan 2 langkah, kemudian 3 langkah ke belakang, dilanjutkan
2 langkah ke depan, kemudian 1 langkah ke belakang, dan akhirnya 1 langkah
ke belakang.
Permasalahan:
a. Dapatkah kamu membuat sketsa lompatan anak tersebut?
b. Tentukanlah berapa langkah posisi akhir anak tersebut dari posisi semula!
c. Tentukanlah berapa langkah yang dijalani anak tersebut!
Alternatif Penyelesaian:
Kita definisikan lompatsaiaan ke depan adalah searah dengan sumbu x positif, dengan
demikian lompatan ke belakang adalah searah dengan sumbu x negatif.
Ke belakang 1 langkah
Ke belakang 1 langkah
Ke depan 2 langkah
Ke belakang 3 langkah
Ke depan 2 langkah
kita misalkan bahwa x = 0 adalah posisi diam si anak.
Anak panah yang pertama di atas garis bilangan menunjukkan, langkah pertama si
anak sejauh 2 langkah ke depan (mengarah ke sumbu x positif), anak panah kedua
menunjukkan 3 langkah si anak ke belakang (mengarah ke sumbu x negatif) dari
posisi akhir langkah pertama, demikianlah seterusnya sampai akhirnya si anak
berhenti pada langkah ke 5.
Jadi, kita dapat melihat pergerakan akhir si anak dari posisi awal adalah 1 langkah
saja ke belakang (x = –1). Banyak langkah yang dijalani si anak merupakan konsep
nilai mutlak, karena kita hanya menghitung banyak langkah, bukan arahnya. Banyak
langkah selalu dinyatakan dengan bilangan bulat positif walaupun arahnya ke arah
sumbu x negatif. Banyak langkah dapat dinyatakan dengan nilai mutlak dari sebuah
bilangan bulat. Misalnya mundur 3 langkah dinyatakan dengan harga mutlak negatif
3 (|-3|). Sehingga banyak langkah anak tersebut adalah |2| + |-3| + |2| + |-1| + |-1| = 9
(9 langkah).
menyelesaikan persamaan nilai mutlak
Nilai mutlak dari suatu bilangan x dapat diartikan sebagai jarak bilangan tersebut terhadap titik 0 pada garis bilangan, dengan tidak memperhatikan arahnya. Ini berarti |x| = 5 memiliki dua selesaian, karena terdapat dua bilangan yang jaraknya terhadap 0 adalah 5: x= –5 dan x = 5 (perhatikan gambar berikut).

Konsep ini dapat diperluas untuk situasi yang melibatkan bentuk-bentuk aljabar yang berada di dalam simbol nilai mutlak, seperti yang dijelaskan oleh sifat berikut.
Sifat Persamaan Nilai Mutlak
Jika X merupakan suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| = k akan mengimplikasikan X = –k atau X = k.
Seperti yang dinyatakan dalam sifat persamaan nilai mutlak, sifat ini hanya dapat diterapkan setelah kita mengisolasi simbol nilai mutlak pada satu ruas. Untuk lebih jelasnya perhatikan contoh berikut.
Contoh 1: Menyelesaikan Persamaan Nilai Mutlak
Selesaikan persamaan: –5|x – 7| + 2 = –13.
Pembahasan Pertama, kita isolasi nilai mutlak, yaitu membuat simbol nilai mutlak berada pada satu ruas sedangkan suku-suku lainnya kita letakkan di ruas yang lain.
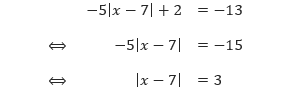
Sekarang perhatikan bahwa x – 7 merupakan “X” pada sifat persamaan nilai mutlak, sehingga

Dengan mensubstitusi ke persamaan semula akan memastikan bahwa himpunan selesaiannya adalah {4, 10}.
Catatan Untuk persamaan seperti pada contoh 1 di atas, hati-hati untuk tidak memperlakukan simbol nilai mutlak seperti tanda kurung biasa. Persamaan –5(x – 7) + 2 = –13 hanya memiliki selesaian x = 10, dan tidak memiliki selesaian kedua karena persamaan tersebut memiliki bentuk sederhana x – 7 = 3. Persamaan –5|x – 7| + 2 = –13 dapat disederhanakan menjadi |x – 7| = 3 yang memiliki dua selesaian.
Persamaan nilai mutlak dapat muncul dari berbagai bentuk. Tetapi dalam menyelesaikan persamaan tersebut, kita harus mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak.
Contoh 2: Menyelesaikan Persamaan Nilai Mutlak
Tentukan himpunan selesaian dari persamaan: |5 – 2/3 x| – 9 = 8.
Pembahasan Dengan mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak, kita mendapatkan
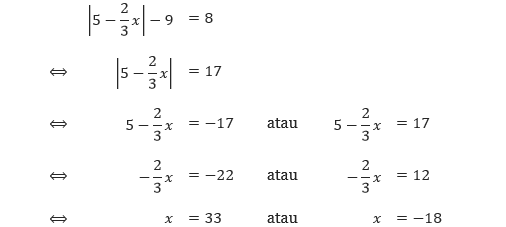
Sehingga, himpunan selesaian dari persamaan tersebut adalah {–18, 33}.
Untuk beberapa persamaan, seringkali kita membutuhkan sifat perkalian persamaan nilai mutlak untuk menyelesaikannya.
Sifat Perkalian Persamaan Nilai Mutlak
Jika A dan B adalah bentuk-bentuk aljabar, maka |AB| = |A||B|.
Perhatikan bahwa jika A = –1 maka menurut sifat tersebut |–B| = |–1||B| = |B|. Secara umum, sifat tersebut berlaku untuk sembarang konstanta A.
Contoh 3: Menggunakan Sifat Perkalian Persamaan Nilai Mutlak
Tentukan selesaian dari persamaan: |–2x| + 5 = 13.
Pembahasan Seperti pada contoh-contoh sebelumnya, kita harus mengisolasi simbol nilai mutlak baru dapat mengaplikasikan sifat-sifat persamaan nilai mutlak.
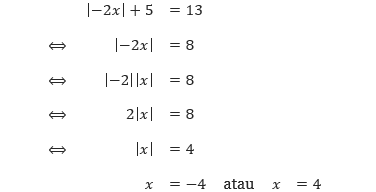
Diperoleh selesaian dari persamaan tersebut adalah x = –4 atau x = 4.
Menyelesaikan Pertidaksamaan Nilai Mutlak “Kurang Dari”
Pertidaksamaan nilai mutlak dapat diselesaikan dengan menggunakan konsep dasar dari sifat persamaan nilai mutlak. Persamaan |x| = 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak 5 dengan titik 0, sedangkan pertidaksamaan |x| < 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak kurang dari 5 dengan titik 0.
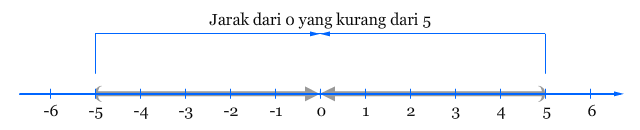
Seperti ilustrasi dari gambar di atas, selesaian dari pertidaksamaan |x| < 5 adalah x > –5 dan x < 5, yang juga dapat dituliskan ke dalam pertidaksamaan gabungan –5 < x < 5. Ilustrasi ini dapat digunakan untuk membangun konsep sifat pertidaksamaan nilai mutlak berikut.
Sifat I: Pertidaksamaan Nilai Mutlak
Jika X adalah suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| < k akan mengimplikasikan –k < X < k.
Contoh: Pertidaksamaan Nilai Mutlak “Kurang Dari”
Tentukan himpunan selesaian dari pertidaksamaan-pertidaksamaan: |3x + 2|/4 ≤ 1 dan |2x – 7| < –5.
Pembahasan Untuk menyelesaikan pertidaksamaan |3x + 2|/4 ≤ 1, kita harus mengisolasi simbol nilai mutlak di satu ruas.
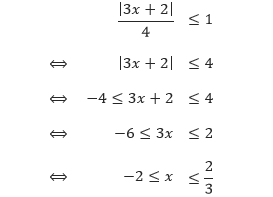
Sehingga, himpunan selesaian dari pertidaksamaan |3x + 2|/4 ≤ 1 adalah { x | –2 ≤ x ≤ 2/3, x bilangan real}. Selanjutnya, perhatikan pertidaksamaan |2x – 7| < –5. Karena nilai mutlak dari setiap bilangan adalah positif atau nol, maka himpunan selesaian dari pertidaksamaan tersebut adalah himpunan koson